Introduction

System overview

The APIS Kalmanfilter (KF) is a APIS ModFrame (MF) module, the class name is BMExKalmanFilter. The KF can be created in the client configuration view, like any other ModFrame component. The Kalmanfilter is a state estimator in which the user can specify a linear or nonlinear state space model in accordance with certain rules. The KF has built in optional bias- and parameter estimation.

The features are:

  • Based on linear or nonlinear state-space models
  • On-line linearization of nonlinear models
  • Bias estimation
  • Parameter estimation
  • Constant or varying Kalmanfilter gain
  • External or internal parameterization
  • Observability checking
  • On-line switching to ballistic mode
  • Easy configuration through the standard ModFrame Client HMI
  • Easy access to all internal Kalmanfilter data structures

Standard Kalman Filter

Model formulation

The linear model formulation is:

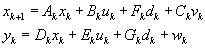
where k denotes the discrete timesteps and

x - State vector
y - Measurement vector
u - Control input vector
d - Disturbance vector
v - Process noise vector
w - Measurement noise vector
A - System transition matrix
B – System control matrix
C – Process noise matrix
D – Measurement state matrix
E – Measurement control matrix
F – State disturbance matrix
G – Measurement disturbance matrix

Kalman filter computations

The following equations are computed at each timestep:

Prediction:

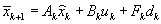
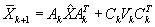
Kalman filter gain:

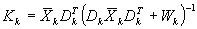
Filtering:

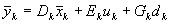
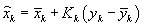
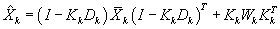
where

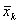  predicted state vector

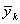  predicted measurement vector

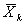 predicted state covariance matrix

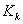 Kalman filter gain matrix

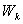 measurement noise covariance matrix

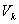  process noise covariance matrix

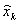  filtered state vector

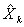 filtered state covariance matrix

Extended Kalman filter

Model formulation

The nonlinear model formulation used in the extended Kalman filter is:

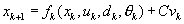
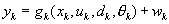
where k denotes the discrete timesteps and

x - State vector
y - Measurement vector
u - Control input vector
d - Disturbance vector
v - Process noise vector
w - Measurement noise vector 
θ – Parameter vector
C – Process noise matrix

Extended Kalman filter computations

The following equations are computed at each timestep:

Prediction:

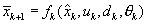
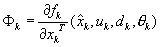
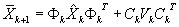
Kalman filter gain:

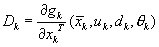
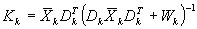
Filtering:

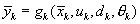
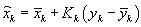
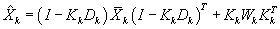
Measurement bias estimation

In order to estimate measurement biases, the internal Kalman filter model is augmented with bias states:

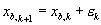
The bias state is added to the original output vector:

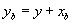
The augmented linear model becomes:

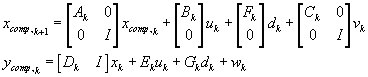
The augmented nonlinear model becomes

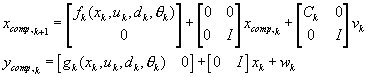
Parameter estimation

The BMExKalmanFilter module implements parameter estimation for nonlinear models. This means that an arbitrary number of the parameters in the general parameter vector θ in the nonlinear model may be estimated.

In order to estimate parameters the internal Kalman filter model is augmented with parameter states:

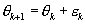
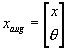
The augmented nonlinear model becomes:

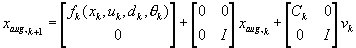
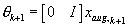
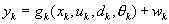
The Kalman filter computations takes place as for the standard Extended Kalman filter, except that

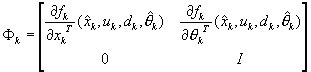
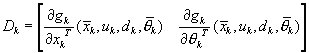
Augmentation sequence

When the Kalman filter is augmented for bias- and parameter estimation, the augmentation sequence is fixed. Assume the following dimensions: 

nmodel - Model state dimension

nbias    - number of estimated biases

nparam - number of estimated parameters

The first part of the state vector is the nmodel original states, the next nbias elements are the estimated output biases, and the last nparam states are the estimated parameters. The resulting augmented state vector is

 

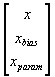
 Project References

  • The Kalmanfilter module is successfully implemented in a paper factory at Norske Skog, Halden, for controlling the paper quality together with the APIS MPC module.
  • In the Ormen Lange gas field, the same modules are used to control the pressure in the two slugcatchers by computing choke setpoints to 16 production chokes located at a distance of 120 km from the slugcatchers.